| |
В. Анохин, А. Ланнэ
MATLAB для DSP. Применение многоскоростных фильтров в задачах узкополосной
фильтрации
Многоскоростные фильтры и банки фильтров (фильтры и банки фильтров
с многочастотной дискретизацией) определили самостоятельное направление
в теории и практике цифровой обработки сигналов (ЦОС). В этой связи
достаточно упомянуть квадратурно-зеркальные фильтры — новый класс
многополосных фильтров, банки многоскоростных фильтров для реализации
вейвлет-преобразований, полифазные фильтры. Многоскоростная фильтрация
нашла широкое практическое применение в задачах компрессии речи, звука
и изображений, построения эффективных систем фильтрации, очистки сигнала
от помех, оптимизации вычислительных ресурсов при реализации алгоритмов
ЦОС.
Для решения задач анализа (моделирования) и синтеза (проектирования)
систем с многочастотной дискретизацией пакет MATLAB предоставляет
широкие возможности. В рамках проекта "MATLAB для DSP" рассмотрим
частную, но практически важную задачу проектирования и моделирования
узкополосного фильтра. Для этих целей, как это и оговорено в проекте,
используются два наиболее дружественных для пользователя инструмента
MATLAB - Simulink и GUI.
Для удобства читателя в первом разделе статьи приведены краткие теоретические
сведения по существу затрагиваемых вопросов. При этом предполагается,
что читатель знаком с предметной областью. В последующих разделах
на примере решения конкретной задачи - синтез и моделирование узкополосного
ФНЧ - излагаются правила и практические рекомендации по использованию
инструментов MATLAB.
Основные соотношения теории многочастотной
дискретизации.
Основы теории многоскоростной фильтрации (многоскоростной обработки
сигналов) и описание приложений можно найти в [1-4].
В качестве базовых при многочастотной дискретизации используются:
- M-кратный дециматор (рис. 1), где YD(n)
= x(Mn);
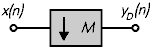
- L-кратный интерполятор (рис. 2), где


Таким образом, частота дискретизации fs сигнала
x(n) связана с частотой дискретизации f's соотношением
Mf's = f's , или соотношением
периодов дискретизации T' = MT. Частоты дискретизации сигналов x(n)
(частота fs ) и yl(n) (частота
fs ) при интерполяции связаны соотношениями f's
= Lfs или T = LT'.
Пример децимации сигнала x(n) при M = 2: отсчёты сигнала до (а) и после
(б) децимации.
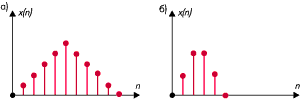 Рис 3.
Рис 3.
Пример интерполяции сигнала x(n) при L = 2: отсчёты сигнала до (а)
и после (б) интерполяции
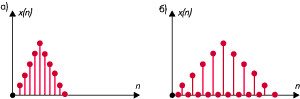 Рис 4.
Рис 4.
При децимации и интерполяции сигнала происходит деформация спектров.
Для децимации
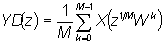
где z = ejw , а
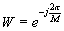
и, следовательно,
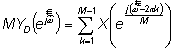
где нормированная частота w = wT', а T' - период дискретизации после
децимации. Он будет в M раз больше, так что в шкале ненормированных
частот получим
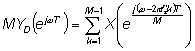
Учитывая, что T' = MT , можно записать окончательное соотношение между
спектрами децимированного сигнала YD(ejw) и исходного X(ejw):
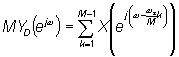
Для интерполяции YI(z) = X(zL) или YI(ejw)
= X(ejwL) или YI(ejw) = X(ejwL).
Таким образом, спектр децимированного сигнала является взвешенной суммой
исходного спектра X(ejw) и его (M–1) сдвинутых по частоте
копий (отражений) с шагом 2Пws/M. Спектр же интерполированного
сигнала является спектром исходного сигнала с изменённым периодом по
частоте. Период увеличивается в L раз.
Учитывая упомянутые выше свойства спектра, необходимо перед децимацией
ставить фильтр децимации, чтобы исключить наложения спектра, а для интерполяции -
фильтр интерполяции для устранения отражений, то есть тех дополнительных
компонент спектра, которые попали в рабочую полосу [0,FN]
за счёт увеличения периода спектра.
Замечательные тождества. При построении систем с многочастотной дискретизацией
очень полезны преобразования, изображённые на рисунках. Они полезны
во многих случаях при реализации фильтров, что будет продемонстрировано
в следующем разделе.
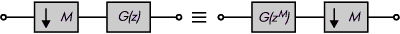 Рис 5.
Рис 5.
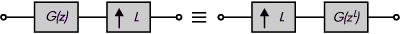 Рис 6.
Рис 6.
Полифазное разбиение и полифазные фильтры. Передаточная функция нерекурсивного
(КИХ - конечной импульсной характеристики) фильтра
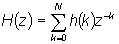
может быть представлено суммой
H(z) = h(0) + h(2)z-2 + ...
+ h(1)z-1 + h(3)z-3 + ... или
H(z) = h(0) + h(2)z-2 + ...
+ z-1 (H(1) + h(3)z-2 + ...) = E0(z2) + E1(z2) .
Смысл многочленов E0 и E1 понятен из контекста.Если
E0 и E1 рассматривать как передаточные функции
КИХ-фильтров, то нетрудно заметить, что базовым элементом задержки таких
фильтров является z-2, обеспечивающий задержку на два такта.
Следовательно, фильтры E0 и E1 могут работать
на частоте дискретизации, в два раза меньшей исходной. Если использовать
разложения по степеням z-3 или z-4 и так далее,
то можно получить блоки фильтров, работающие на ещё более низких частотах
дискретизации. Итоговая схема фильтра, когда H(z) = E0(z2) + z-1E1(z2)
,показана на рисунке 7.
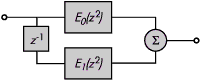
Рассмотренное разбиение называется полифазным, а реализующие его схемы -
полифазными фильтрами.В качестве примера, иллюстрирующего построение
полифазного фильтра и использование замечательных тождеств, покажем,
как можно эффективно реализовать КИХ-фильтр дециматор.
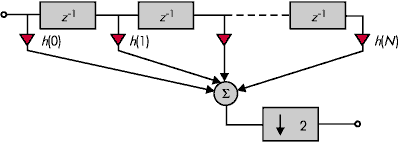 Рис 8.
Рис 8.
В схеме рис. 8 для вычисления каждого отсчёта необходимо выполнить
N+1 умножений и N сложений. В то же время, за счёт децимации (M = 2)
половину результатов отсчётов мы отбрасываем и, следовательно, используем
ресурсы вычислителя неэффективно.Построим фильтр на основе полифазного
разбиения (полифазный фильтр, рис. 7) и воспользуемся замечательным
тождеством (рис. 5). Последовательность преобразований при этом показана
на рис. 9.
 Рис. 9
Рис. 9
В результате фильтры E0(z2) и E1(z2),
работающие на частоте fs, заменяются фильтрами E0(z)
и E1(z), работающими на частоте fs/2. Таким образом
мы получим двукратную эконом ию в скорости вычислений. При коэффициенте
децимации M применение полифазных фильтров позволяет получить экономию
в M раз. Аналогичные результаты получаются и при полифазном построении
фильтров интерполяторов [1,2]. Таким образом, полифазные реализации
в совокупности с рациональными преобразованиями схем фильтров позволяют
строить эффективные вычислители в задачах ЦОС.
Расчёт узкополосного низкочастотного фильтра.
В процессе цифровой обработки сигналов нередко возникает задача фильтрации
сигнала в очень узком частотном диапазоне. Примером такой задачи может
служить ситуация, когда сигнал содержит несколько составляющих на близких
частотах, и требуется выделить одну из них. Для этого необходимо спроектировать
цифровой фильтр с очень узкими относительными полосами пропускания и
перехода. В зависимости от расположения составляющих сигнала, это может
быть фильтр нижних, верхних частот, полосовой или заграждающий фильтр.
Прямое проектирование таких устройств часто приводит к фильтрам очень
высоких порядков, практическая реализация которых либо нерациональна,
либо невозможна.
Рассмотрим следующий пример. Пусть имеется дискретный сигнал
u(n) = sin(2πf1nT) + sin(2πf2nT)
+ e(n) ,
где f1 = 90 Гц и f2 = 105 Гц - частоты составляющих;
T = 1/fs = 1/8000 с - период дискретизации; fs = 8000 Гц -
частота дискретизации; e(n) - гауссовский шум с нулевым средним и дисперсией
σ2 = 0,1. Требуется выделить синусоидальную составляющую
с частотой f1. Для этого необходимо построить фильтр нижних
частот с граничными значениями частот полосы пропускания fpb
и полосы задерживания fsb, удовлетворяющими условию f1 <
fpb< fsb < f2 . Поскольку частота
Найквиста fN = fs/2 = 4000 Гц, для нормализованных
значений fpb = fpb/fN и fsb
= fsb/fN это условие будет выглядеть так :
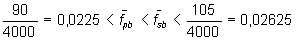
Следовательно, переходная полоса Δf амплитудно-частотной характеристики
фильтра (АЧХ) не должна превышать величину Δf < 0,02625 – 0,0225
= 0,00375. Эти требования схематически показаны на рис. 10.
Для решения сформулированной задачи попробуем спроектировать нерекурсивный
фильтр с полосой пропускания от 0 до 95 Гц и полосой задерживания от
100 до 4000 Гц, то есть до частоты Найквиста. Кроме того, потребуем,
чтобы АЧХ в полосе пропускания находилась в пределах [0,99, 1,01], а
в полосе задерживания не превышала значения 0,0001. Для этого нам необходимо
воспользоваться функциями пакета MATLAB, оценивающими по заданным требованиям
порядок фильтра и рассчитывающими его коэффициенты. Эти действия удобно
выполнять с помощью графической программы (GUI) sptool, входящей в библиотеку
signal пакета MATLAB и описанную в [5]. Загрузим эту программу с помощью
инструкции sptool и на появившейся главной панели нажмём кнопку New
Design, находящуюся под окном Filters. После этого на экране появится
панель Filter Designer.
Чтобы рассчитать фильтр, надо ввести данные в поля Sampling Frequency:
Fp (верхнее граничное значение полосы пропускания), Rp (максимально
допустимая величина пульсаций в полосе пропускания), Fs (нижнее граничное
значение полосы задерживания) и Rs (максимально допустимая величина
пульсаций в полосе задерживания). Как видно, соответствующие значения
пульсаций, вводимые в поля Rp и Rs, должны быть заданы в децибелах (вводятся
абсолютные величины). Введём данные, необходимые для расчёта нашего
фильтра:
-
8000 - в поле Sampling Frequency;
-
95 и 100 - в поля Fp и Fs, соответственно;
-
20*log10(1,01)–20*log10(0,99) - в поле Rp;
-
80 - в поле Rs, что соответствует ослаблению в
10000 раз.
После нажатия на кнопку Apply появится предупреждение, что оценочное
значение порядка проектируемого фильтра 5022 слишком велико, и дальнейшая
процедура расчёта может дать непредсказуемые результаты. Однако даже
если такой фильтр построен, для его применения потребуется очень большой
вычислительный ресурс. Так как коэффициенты фильтра обладают симметрией
и общее их количество равно 5023, процессор должен выполнять
(5022/2 + 1) MACs/sample х 8000 samples/sec = 20096000 MACs/sec
(Multiply-And-aCcumulate operations per second - число операций умножения-накопления
в секунду, показатель быстродействия процессора). Для хранения коэффициентов
потребуется 2512 ячеек памяти.
Альтернативный путь решения рассматриваемой задачи заключается в использовании
идей многочастотной дискретизации - последовательном прохождении сигнала
через полифазные фильтры. Как было показано, каждый из них выполняет
две функции: фильтрацию в заданной полосе и изменение частоты дискретизации
выходного сигнала. Прежде всего, для восстановления отфильтрованного
сигнала [0, 90] Гц (сигнал содержит только составляющую на частоте 90 Гц),
его достаточно дискретизировать с частотой, большей или равной fs1
= 2·90 = 180 Гц. Для выделения составляющей с частотой fs
выполним фильтрацию сигнала, используя два полифазных фильтра-дециматора
и два полифазных фильтра-интерполятора. Пусть первый фильтр имеет полосу
пропускания
[0, 1/20–0,025]·FN = [0, 100] Гц
и полосу задерживания
[1/20, 1]·FN = [200, 4000] Гц.
АЧХ в полосе пропускания этого фильтра должна находиться в пределах
[0,995, 1,005], а в полосе задерживания - не превышать величину 10-4.
Исходя из этих требований, коэффициент децимации М положим равным 20.
При этом частота дискретизации на выходе первого фильтра дециматора
будет равна 8000/20 = 400 Гц.
Расчёт коэффициентов первого фильтра можно выполнить опять с использованием
GUI sptool. Вводимые данные для расчёта:
-
8000 - в поле Sampling Frequency;
-
100 и 200 - в поля Fp и Fs, соответственно;
-
20*log10(1,005)–20*log10(0,995) или 0,08686 - в
поле Rp;
-
80 - в поле Rs, что соответствует ослаблению в
10000 раз.
Результаты расчёта дают приблизительную оценку порядка
фильтра n1 = 270, однако полученные значения Actual Rp = 0,1436
и Actual Rs = 75,58 (они отображаются в правой части окна Filter Designer)
указывают на необходимость увеличить порядок фильтра и повторить вычисления.
В нашем примере мы выбрали значение n1 = 289, что соответствует
Actual Rp = 0,08281 и Actual Rs = 80,16.
Второй фильтр дециматор характеризуется следующими параметрами:
-
400 в поле Sampling Frequency;
-
95 и 100 в полях Fp и Fs, соответственно;
-
0,08686 в поле Rp;
-
80 в поле Rs, что соответствует ослаблению в 10000 раз.
Результаты вычислений дают предварительную оценку порядка фильтра n2 = 270
и фактические значения Rp и Rs для этого порядка, которые опять-таки
не укладываются в заданные требования (пульсации недопустимо большие).
Выбор n2 = = 275 обеспечивает выполнение требований.
Чтобы коэффициенты спроектированных фильтров стали доступны для дальнейшего
использования, их надо экспортировать в рабочее пространство MATLAB.
Для этого необходимо открыть меню File главной панели sptool и выбрать
раздел Export… Если экспортированные структуры имеют имена filt1 и filt2,
извлечь соответствующие коэффициенты можно с помощью команд
b1=filt1.tf.num;
b2=filt2.tf.num;
Применение двух фильтров дециматоров, реализуемых в виде полифазных
структур, требует выполнения
290/2 MACs/с · 8000 отсчётов/с · 1/20 + 276/2 MACs/с · 400 отсчётов/с
· = 85600 MACs/с ,
и хранения 145 + 138 = 283 коэффициентов.
Для восстановления исходной частоты дискретизации 8000 Гц следует
к выходу второго фильтра последовательно подключить два фильтра-интерполятора,
причём коэффициент интерполяции первого фильтра равен 2, а второго -
20. С учётом того, что эти фильтры выполняют столько же операций в
секунду, сколько и предшествующие им фильтры- дециматоры, общее количество
операций умножения с накоплением в секунду будет равно 85600·2 = 171200,
а число коэффициентов фильтров - 283.
Моделирование узкополосного низкочастотного
фильтра
Описанная процедура может быть легко реализована в виде модели Simulink,
для чего нам потребуются следующие блоки:
-
генератор синусоидальных колебаний Sine Wave (папка
Simulink\ Sources);
-
генератор шума Random Number (Simulink\Sources);
-
сумматор Sum (Simulink\Math);
-
полифазный фильтр-дециматор FIR Decimation (DSP
Blockset\Filtering\ Multirate Filters);
-
полифазный фильтр-интерполятор FIR Interpolation
(DSP Blockset\ Filtering\Multirate Filters);
-
анализатор спектра Buffered FFT Frame Scope (DSP
Blockset\DSP Sinks);
-
осциллограф Scope (Simulink\Sinks).
Правила построения моделей подробно изложены в справочной системе
MATLAB, с ними также можно ознакомиться, обратившись к соответствующим
источникам [6-8].
Построенная модель, где блоки (F+D)1 и (F+D)2 - это фильтры-дециматоры,
а блоки (I+F)1 и (I+F)2 - фильтры-интерполяторы. Перед тем, как её запустить,
необходимо задать параметры блоков и режима работы модели. В нашем примере
параметры блоков имеют следующие значения:
-
Блок (F+D)1. FIR filter coefficients = b1, Decimation
factor = 20;
-
Блок (F+D)2. FIR filter coefficients = b2, Decimation
factor = 2;
-
Блок (I+F)2. FIR filter coefficients = b2, Interpolation
factor = 2;
-
Блок (I+F)1. FIR filter coefficients = b1, Interpolation
factor = 20;
-
Анализаторы спектра 1 и 5. Параметры блоков одинаковы
и указаны на рис. 13;
-
Анализаторы спектра 2 и 4. FFT length и Buffer size = 256,
Sample time of original time series = 20/8000, остальные - как на
рис. 13;
-
Анализатор спектра 3. FFT length = = 256 и Buffer
size = 128, Sample time of original time series = 20·2/8000, остальные -
как на рис. 13;
-
Генератор 1. Amplitude = 1, Frequency = 90, Sample
Mode = Discrete, Sample Time = 1/8000;
-
Генератор 2. Amplitude = 1, Frequency = 105, Sample
Mode = Discrete, Sample Time = 1/8000;
-
Генератор шума. Mean = 0, Variance = 3e-1, Sample
Time = 1/8000.
Параметры режима работы модели устанавливаются в окне
Simulation Parameters.
Заключение
Рассмотренный пример наглядно демонстрирует возможности многочастотной
дискретизации для решения важных практических задач. Действительно,
относительно узкополосные фильтры являются важнейшим элементом радиосистем
и в этом смысле имеют большое самостоятельное значение. Помимо этого,
многочастотная дискретизация весьма эффективна для построения банков
фильтров и для решения задач обработки сигналов с помощью техники
вейвлет-разложений.
Литература
1. Vaidyanathan P.P. Multirate Systems and Filter Banks. Prentice
Hall. Englewood Cliffs. NY, 1993.
2. Вайдьнатхан П.П. Цифровые фильтры, блоки фильтров и полифазные
цепи с многочастотной дискретизацией. Методический обзор. ТИИЭР, 1990.
т. 78. № 3. С. 77–120.
3. Гольденберг Л.М., Матюшкин Б.Д., Поляк М.Н. Цифровая обработка
сигналов. М.: Радио и связь, 1985.
4. Витязев В.В. Цифровая частотная селекция сигналов. М.: Радио и
связь, 1993.
5. Андреев И.В., Ланнэ А.А. MATLAB для DSP: SPTool - инструмент для
расчёта цифровых фильтров и спектрального анализа сигналов // Цифровая
обработка сигналов. 2000. № 2. С. 6–13.
6. Дьяконов В.П., Абраменкова И.В. Matlab 5.0/5.3. Система символьной
математики. М.: “Нолидж”, 1999.
7. Гультяев А.К. Имитационное моделирование в среде Windows. СПб.:
КОРОНА принт, 1999.
8. Анохин В.В. Моделирование аналого-цифрового преобразования. В 2-х
частях. // Chip-News. 2000. № 2. С. 4–7. Chip-News. 2000. № 3. С.
26–29.
|