| |
М. Горлов, А. Строгонов
Геронтология кремниевых интегральных схем. Часть 2
Прогнозирование долговечности ИС по параметрическим отказам
Использование метода Бокса-Дженкинса (применяемого для анализа и прогнозирования нестационарных случайных процессов и временных рядов различной природы) для описания процесса деградации параметров ИС основано на том факте, что результирующий случайный процесс деградации параметров ИС нестационарен и может быть представлен в виде композиции необратимой случайно-детерминированной (полуслучайной) величины Xсд(t) и обратимой случайно-варьирующей составляющей Xсв(t). В общем виде изменение параметра X(t) во времени можно записать как: X(t) = Xсд(t) + Xсв(t). Случайно-детерминированная составляющая Xсд(t) обусловлена причинным механизмом, определяющим направление и скорость процесса. Дрейф параметра при наличии необратимого детерминированного процесса имеет постоянное монотонное направление. Монотонность сохраняется, если ведущий причинный механизм действует постоянно. Нарушение плавного хода функции, смена направления процесса означают или смену действующего механизма, или значительное накопление изменений, ведущее к качественному скачку в состоянии объекта, что может быть зафиксировано как отказ.
Применение теории временных рядов для изучения долговечности ИС есть результат подхода к исследуемой ИС как к “чёрному ящику”. Такой подход ставит своей целью посредством построения некоторой модели установить изоморфизм не с внутренней структурой и её функционированием, а с внешними проявлениями её информативных параметров. Метод “чёрного ящика” — кибернетический, то есть объект исследования представляется как некоторая кибернетическая система, которая может быть описана своим функциональным оператором.
Впервые метод Бокса-Дженкинса был применён в работе для прогнозирования поведения статических характеристик тестовых ИС в течение небольшого промежутка времени в температурных и электрических режимах, соответствующих условиям испытаний на безотказность. Были построены модели деградации ИС относительно характеристики входного тока закрытой схемы I1 . Во всех случаях процесс деградации параметра I1 описывался моделью АРПСС (0,1,1). Метод получил дальнейшее развитие для прогнозирования индивидуальной надёжности лазеров по параметрическим отказам.
Метод Бокса-Дженкинса основывается на том, что гладкий нестационарный временной ряд путём взятия разностей некоторого d-го порядка можно свести к эквивалентному стационарному, то есть к случаю, для которого разработаны методы анализа и прогнозирования. В методе Бокса-Дженкинса нестационарный временной ряд представляется в виде модели авторегрессии проинтегрированного скользящего среднего (АРПСС) в прямой и возвратной формах:
Прямая форма:
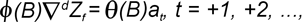
Возвратная форма:
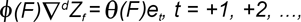
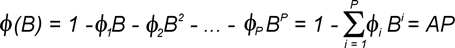
— оператор,
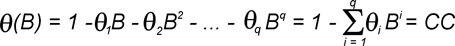
— оператор,
где ф(B), ф(F) — операторы авторегрессии (АР); B, F — операторы сдвига; С — оператор разности: 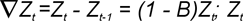 ; Zt — нестационарный временной ряд деградирующего параметра ИС; d — порядок разности, обеспечивающий переход от нестационарного ряда к эквивалентному стационарному; p — порядок авторегрессии; q, q(B), q(F) — порядок и операторы проинтегрированного скользящего среднего (СС), соответственно; at, et — последовательности независимых случайных величин, имеющих одинаковое нормальное распределение (белый шум). ; Zt — нестационарный временной ряд деградирующего параметра ИС; d — порядок разности, обеспечивающий переход от нестационарного ряда к эквивалентному стационарному; p — порядок авторегрессии; q, q(B), q(F) — порядок и операторы проинтегрированного скользящего среднего (СС), соответственно; at, et — последовательности независимых случайных величин, имеющих одинаковое нормальное распределение (белый шум).
Метод Бокса-Дженкинса эффективен только в том случае, если длина временного ряда (число замеров) не меньше 30 условных равных единиц наработки. Как же быть в том случае, если испытания дороги, проводятся длительное время (свыше 10 лет), число замеров мало или достаточно, но проводились они не в равные интервалы времени? Например, временной ряд замеров параметров ИС типа 106ЛБ1 при испытаниях на долговечность в течение 120 тыс.ч. согласно действующим стандартам имеет вид: 0; 1; 2; 3; 4; 5; 6; 7; 8; 9; 10; 11; 12; 13; 14; 15; 16; 17; 18; 19; 20; 21; 22; 23; 24; 25; 26; 27; 28; 29; 30; 40; 50; 60; 70; 80; 90; 100; 110; 120 тыс.ч. В этом случае, для получения значений параметров в равные интервалы времени необходимо прибегнуть к специальной процедуре получения недостающих значений. Естественно, что такие операции над временными рядами могут вносить существенные погрешности и даже изменить природу временного ряда. Следует учесть, что повторить эксперимент такой длительности (для большей достоверности) практически невозможно, а если повторить его на другой выборке, то будем иметь дело с совершенно другой кривой (траекторией) процесса деградации, так как за эти годы произошли конструктивно-технологические изменения этой схемы.
Одним из преимуществ метода Бокса-Дженкинса перед другими методами прогнозирования является то, что он позволяет построить модели временных рядов деградации параметров ИС, которые можно использовать для прогнозирования долговечности схем по параметрическим отказам. Это явилось предпосылкой к дальнейшему исследованию возможности использования метода, а именно: возможно ли подобрать универсальные модели для описания деградации логических параметров кремниевых биполярных ИС. Для этого была поставлена задача, состоящая из трёх этапов: 1 — на основе наиболее “длинного” временного ряда деградации по испытаниям на долговечность установить обобщённый вид модели для таких основных параметров, как выходные напряжения низкого (UOL) и высокого уровней (UOH); 2 — апробировать их на статистических данных по испытаниям ИС разных типов с различной длительностью; 3 — применить к другим видам испытаний (например, ускоренным). В ходе этапов требовалось осуществить прогнозирование долговечности ИС до наступления параметрических отказов и сравнить с реальными данными по испытаниям на долговечность.
Для подбора АРПСС-моделей использовалась схема, основанная на стандартном порядке анализа временных рядов. Оценка параметров АРПСС-моделей проводилась с использованием статистического пакета программ Statistica for Windows, процедура “Анализ временных рядов”. В данной работе за параметрический отказ принято достижение верхней (для параметра UOL) или нижней (для параметра UOH) границы с 90-% доверительным интервалом прогнозируемых значений уровня отказов, установленного в ТУ. Согласно этой схеме, осуществлено прогнозирование долговечности по наихудшим значениям параметров UOL и UOH ИС типа 106ЛБ1 и 134ЛБ1 по наработке 70–120 тыс.ч., типов 1804ИР1, 134РУ6 — по наработке 25 тыс.ч., и типа 582ИК1 — по наработке 40 тыс.ч. (табл. 1).
Таблица 1. Результаты прогнозирования времени наступления параметрического отказа по параметрам UOL и UOH ИС типов 106ЛБ1, 134ЛБ1Б 134РУ6, 180ИР1, 582ИК1
| Параметр |
Вид модели АРПСС |
Прогнозируемая долговечность
ИС в выборке до
наступления первого
отказа с учетом 90-%
доверительных
интервалов,
тыс.ч* |
| ИС типа10ЛБ1, 120 тыс.ч. испытаний (январь 1980) |
| UOL |
АРПСС(0,1,2): С'Zf = a1-0,228af-1-0,538af-2+(0,017)2 |
150 |
| UOH |
АРПСС(0,1,5): С'Zf = a1+0,282af-1+0,485af-2+0,450af-3+0,322af-4+0,670af-5+|0,017)2 |
130 |
| ИС типа 134ЛБ1, 110 тыс.ч. испытаний (ноябрь 1981) |
| UOL |
АРПСС(0,1,1): С'Zf =a1-0,718af-1+(0,002)2 |
>300 |
| UOH |
АРПСС(2,1,0): С'Zf +0,685С'Zf-1+0,334С'Zf-2=af+(0,082)2 |
215 |
| ИС типа 134ЛБ1, 70 тыс.ч. испытаний (октябрь 1981) |
| UOL |
АРПСС(0,1,1): С'Zf= af-0,718af-1+(0,002)2 |
>300 |
| UOH |
АРПСС(2,1,0):С'Zf+0,657С'Zf-1+0,323С'Zf-2=af+(0,018)2 |
>300 |
| ИС типа 134РУ6, 25 тыс.ч. испытаний (май 1988) |
| UOL |
АРПСС(0,2,2):С2Zf= af+0,250af-1+0,663af-2+(0,002)2 |
>300 |
| ИС типа 180ИР1, 25 тыс.ч. испытаний (декабрь 1987) |
| UOL |
АРПСС(0,1,1):С'Zf= af+0,869af-1+(0,004)2 |
50 |
| UOH |
АРПСС(1,1,0):С'Zf-0Б868С'Zf-1=af+(0,001)2 |
275 |
| ИС типа 582ИК1, 40 тыс.ч. испытаний (ноябрь 1986) |
| UOL |
АРПСС(0,2,1):С'Zf=af+0,436af-1+(0,012)2 |
53 |
*) - недостающие значения получены апроксимацией кубическими сплайнами.
В результате, на основе изучения поведения параметров UOL и UOH ИС типов 106ЛБ1, 134ЛБ1, 134РУ6, 1804ИР1 и 582ИК1А, было сделано предположение, что деградация наихудших значений параметра UOH описывается обобщённой моделью АРПСС(0,d,q), а параметр UOH — моделью АРПСС(p,d,0), где d, q и p принимают значения “1” или “2”.
С целью подтвердить или опровергнуть достоверность прогнозов деградации параметров UOL и UOH ИС типа 106ЛБ1 выпуска января 1980 года при испытаниях на долговечность продолжительностью 120 тыс.ч., был проведён контрольный замер параметров этих же ИС по прошествию 10 тыс.ч. Таким образом, фактическая наработка этих ИС при испытаниях на долговечность составила 130 тыс.ч. Отказов за это время не зафиксировано.
Сравнение прогнозов, построенных с использованием АРПСС-моделей с контрольной точкой (КТ), показывает, что прогнозируемое время наступления параметрического отказа по параметрам UOL и UOH по наработке 120 тыс.ч. оказалось занижено. Однако, КТ укладывается в 90-% доверительный интервал для параметра UOL (рис. 1) и находится на верхней границе 90-% доверительного интервала для параметра UOH. Согласно прогнозам модели АРПСС(0,1,5), для параметра UOH ожидался параметрический отказ в выборке, но он не был зафиксирован.
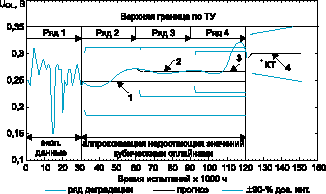
Рис. 1. Графическая верификация прогнозов модели АРПСС(0,1,2) для наихудших значений параметра UOL в выборку ИС типа 106ЛБ1, при испытаниях на долговечность в течение 120 тыс.ч. (недостающие значения получены аппроксимацией кубическим сплайном): 1 - прогноз для ряда 1; 2 - прогноз для ряда 2; 3 - прогноз для ряда 3; 4 - прогноз для ряда 4
В табл. 2 приведены результаты прогнозирования времени наступления параметрического отказа по параметру UOL по данным испытаний на долговечность в течение 130 тыс.ч. На рис. 2 показан процесс деградации параметра UOL при прогнозировании на глубину 30 тыс.ч. по наихудшим, средним и наилучшим значениям в выборке, при различных методах аппроксимации. Это сделано с целью сравнения влияния методов получения недостающих значений на точность прогнозов. Сравнивая табл. 1 и 2, видим, что вид модели АРПСС для параметра UOL по наихудшим значениям не меняется для разных методов аппроксимации недостающих значений.
Таблица 2. Результаты прогнозирования времени наступления параметрического отказа по параметру UOL ИС типа 106ЛБ1 выпуска января 1980 года на глубину 30 тыс.ч.
| Вид модели АРПСС |
Время наступления параметрического отказа, тыс.ч.* |
| Аппроксимация кубическими сплайнами: |
| Наихудшие значения (0,1,2):С'Zf=af-0,236af-1-0,578af-2 |
не наступает |
| Метод интерполяции: |
| Наихудшие значения (0,1,2):С'Zf=af-0,291af-1-0,557af-2 |
не наступает |
| Минимальные значения (0,1,1):С'Zf=af-0,721af-1 |
не наступает |
| Наилучшие значения (0,1,1):С'Zf=af-0,656af-1 |
не наступает |
*) - прогнозируемая долговечность ИС с учетом 90-% доверительного интервала.
Таким образом, результаты прогнозирования времени наступления параметрического отказа в выборке по наихудшим значениям параметров UOL и UOH ИС типа 106ЛБ1 можно признать удовлетворительными.
Методика прогнозирования, апробированная на ряде ИС, выпускаемых одним заводом-изготовителем, была использована для прогнозирования долговечности ИС типа 136ЛА3 (другого завода изготовителя), фактическая наработка которых составила 90 тыс.ч. по наихудшим значениям параметров UOL и UOH. За время испытаний не было зафиксировано ни одного отказа. Объём выборки по каждому типу ИС составил 20 шт.
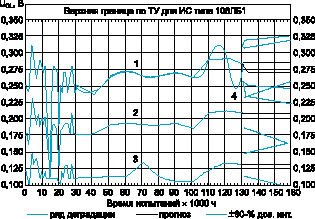
Рис. 2. Прогнозирование долговечности параметра UOL в выборке ИС типа 106ЛБ1, при испытаниях на долговечность в течение 130 тыс.ч. (недостающие значения получениы интерполяцией): 1 - наихудшие значения; 2 - средние значения и 4 - наихудшие значения (недостающие значения получениы кубическими сплайнами)
Предварительно предполагалось из-за идентичности конструктивно-технологических особенностей ИС серий 136 и 134, что временные ряды деградации параметров ИС серии 136 должны описываться теми же моделями АРПСС, что и временные ряды деградации параметров ИС серий 134. Однако, ввиду недостаточности экспериментальных данных (при испытаниях на долговечность ИС типа 136ЛА3 контрольные замеры проводились с интервалом времени 0, 20, 25, 30, 35, 40, 45, 50, 60, 80 и 90 тыс.ч.) не представляется возможным провести анализ временных рядов сразу, так как для этого необходимо как минимум 30 экспериментальных точек. Для получения значений ряда в равные интервалы времени также использовались процедуры получения недостающих значений, например, вместо 11 экспериментальных точек формировалась 91 точка с шагом 1 тыс.ч.
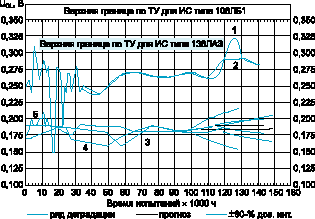
Рис. 3. Поведение параметра UOL ИС типа 106ЛБ1 (кривая 1 - недостающие значения получены аппроксимацией кубическими сплайнами, 2 - интерполяцией) при испытаниях на долговечность в течение 130 тыс.ч.; ИС типа 136ЛА3 - при испытаниях на сохраняемость в течение 12 лет (кривая 3) и долговечность 90 тыс.ч. (кривая 4); при испытаниях на долговечность ИС типа 134ЛБ1 в течение 110 тыс.ч. (кривая 5)
Для ИС серии 106 и 136 из-за конструктивно-технологических различий характерно колебание параметра UOL относительно верхних границ уровней отказов (рис. 3). На рис. 3 показано поведение параметра UOL ИС типа 106ЛБ1 при испытаниях на долговечность в течение 130 тыс.ч.; ИС типа 136ЛА3 — сохраняемость в течение 12 лет и долговечность 90 тыс.ч.; ИС типа 134ЛБ1 — на долговечность в течение 110 тыс.ч., а также результаты прогнозирования деградации параметра UOL ИС типа 136ЛА3 с использованием модели АРПСС(1,1,0) и с уточнённой моделью для ИС 134ЛБ1 — АРПСС(0,1,3) на глубину 30 тыс.ч. Хотя поведение временных рядов деградации параметра UOL ИС типов 134ЛБ1 и 136ЛА3 схоже (траектории процесса деградации переплетаются), тем не менее, подобранные АРПСС-модели различны.
Прогнозируемая долговечность ИС типа 136ЛА3 по наихудшему значению в выборке параметра UOL с использованием разных моделей АРПСС оценивается величиной не хуже 150 тыс.ч.
Тел.: (0732) 77 3714
E-mail: mart@fil1.vrn.ru
|